(20210830) FFT with CMSIS-DSP Library

i have completed the ground work for making Fast Fourier Transform (FFT) available via the CMSIS DSP Library.

the reason i chose the CMSIS DSP Library to perform FFT is that it is highly optimized for Arm Cortex-M processors ( i.e STM32F4 + STM32H7 ) and it already ships with the STM32duino project as part of the general CMSIS Library.

usage is quite straigth forward and did not pose too much of a challenge. the steps to perform a FFT analysis are as follows:

• include CMSIS DSP Library with #include <CMSIS_DSP.h>
• allocate buffers
  • in- and output buffers
  • optional buffer for power or energy ( which is half the size of the former buffers )
• initialize real FFT instance
  • this only needs to be done once
  • real ( instead of complex ) FFT suffices for audio signals
• analyze input buffer and store result in output buffer with arm_rfft_fast_f32()
• convert complex numbers from output buffer to energy or power values with arm_cmplx_mag_f32
• optionally find the peak frequency bin with arm_max_f32

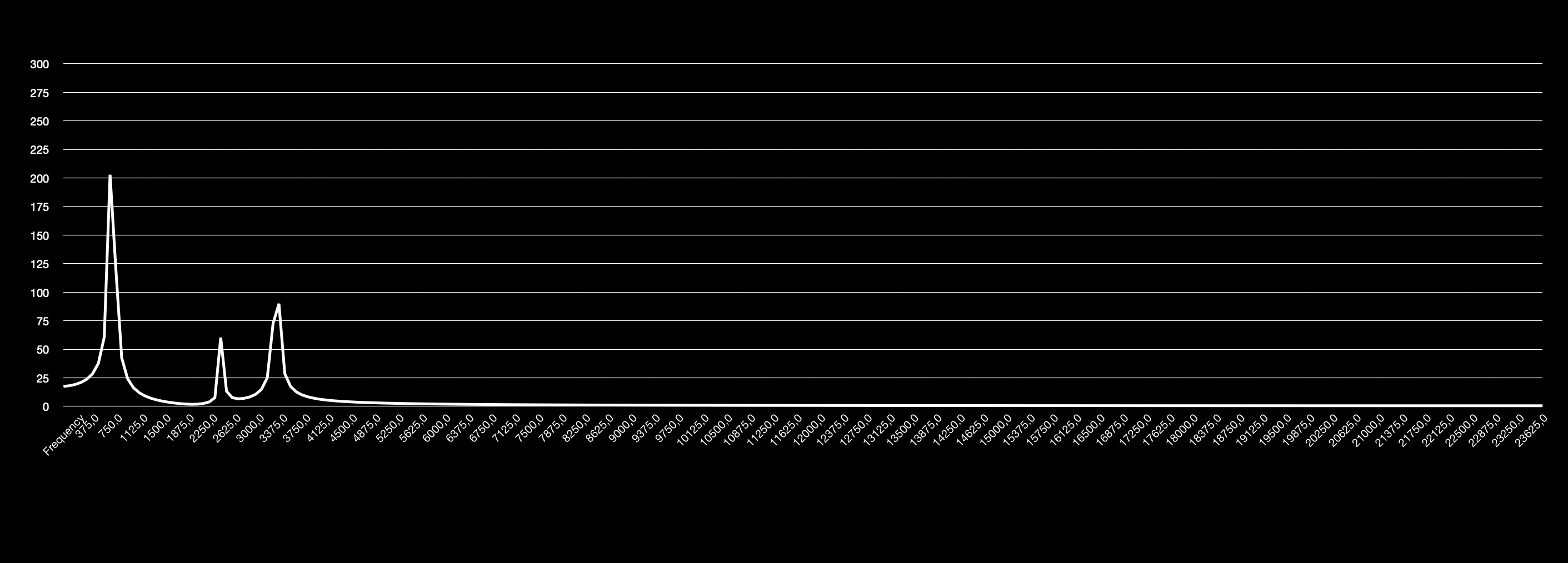
below is a working example that performs an FFT analysis on a chunk of sample data which contains a signal with 3 blended sine wave tones at frequencies 880Hz, 2640Hz and 3520Hz, and finds the most dominant frequency:

#include <CMSIS_DSP.h>

#define SAMPLE_BUFFER_LENGTH        4096
#define SAMPLE_BUFFER_LENGTH_HALF   (SAMPLE_BUFFER_LENGTH/2)
#define SAMPLING_RATE               48000

float fft_input[SAMPLE_BUFFER_LENGTH];
float fft_output[SAMPLE_BUFFER_LENGTH];
float fft_power[SAMPLE_BUFFER_LENGTH_HALF];

uint8_t     ifftFlag                = 0;
float       frequency_resolution    = (float)SAMPLING_RATE / (float)SAMPLE_BUFFER_LENGTH;

void setup() {
    /* write signal to array */
    for (int i = 0; i < SAMPLE_BUFFER_LENGTH; i++) {
        float r = (float)i / (float)SAMPLING_RATE;
        r *= 3.14159265359 * 2;
        r *= 880; // frequency in Hz
        float s = sin(r) + sin(r * 4) * 0.5 + sin(r * 3) * 0.25;
        fft_input[i] = s;
    }

    /* analyze signal */
    arm_rfft_fast_instance_f32 fft;
    arm_rfft_fast_init_f32(&fft, SAMPLE_BUFFER_LENGTH);
    arm_rfft_fast_f32(&fft, fft_input, fft_output, ifftFlag);
    arm_cmplx_mag_f32(fft_output, fft_power, SAMPLE_BUFFER_LENGTH_HALF);
    for (int i = 1; i < SAMPLE_BUFFER_LENGTH_HALF; i++) {
        Serial.printf("%i\tfrq: %.1f\tenergy %.6f\r\n", i, i * frequency_resolution, fft_power[i]);
    }
    
    /* find dominant frequency */
    float32_t   maxValue;
    uint32_t    maxIndex;
    arm_max_f32(fft_power, SAMPLE_BUFFER_LENGTH_HALF, &maxValue, &maxIndex);
    Serial.printf("\r\n");
    Serial.printf("max power: %f\r\n", maxValue);
    Serial.printf("max index: %i\r\n", maxIndex);
    Serial.printf("frequency: %f\r\n", (maxIndex * frequency_resolution));
}

CMSIS in desktop simulator (SDL)

things turned a bit ugly when i tried to use the CMSIS-DSP Library on the desktop platform. CMSIS is obviously designed to be comiled for Arm MCUs only ( e.g STM32F4 is based on Arm Cortex-M4 + STM32H7 on Arm Cortex-M7 architecture ). fortunately in more recent versions of the CMSIS Library ( v5.8.1 ) and CMSIS-DSP Library ( v1.10.0 ) it is also possible to compile against other CPUs ( i.e Intel Core i7 ).

this allowed me to use the FFT analysis code from CMSIS-DSP Library. however, it took a bit of extra work to edit move things around to make it compatible with the arduino build environment. fortunately this all works now. i have included a slimmed down version the CMSIS-DSP Library reduced to FFT functionality in the desktop platform.

Considerations for a NodeFFT Class

a few things are worth noting and considering when implementing an FFT node in Klang or Strom:

although the frequencies evaluated by the FFT analysis range from 0Hz to SAMPLING_RATE/2Hz ( i.e 48000Hz ) which is well sufficient, the number of bands is only SAMPLE_BUFFER_LENGTH/2 ( i.e 128 samples = 64 bands ). this means if the sample buffer length is defined as 128 samples each of the 64 bands covers a frequency range of 375Hz ( = 48000Hz / 128 samples ). this is a pretty low resolution, especially in the lower regions of the frequency spectrum and would not suffice for a lot of possible applications.

one obvious and naive measure to address this problem is to increase the number of samples by collecting sampling buffers and only analyze e.g every 32nd frame. in this example the range would be reduced from 375Hz to approx 12Hz. of course the downside of this approach is that the update frequency of the analyzed values is reduced from 375Hz to approx 12Hz as well.

i know i am not the first to contemplate this question ( e.g How to increase resolution of FFT? ) and would be really interested in more research on this.